Coordination Compounds
Topics:Werner's Theory of Coordination Compounds & Definition of Important Terms in Coordination Compounds
- Coordination Compounds − Complex compounds in which transition metal atoms are bound to a number of anions or neutral molecules
Postulates of Werner’s Theory of Coordination Compounds
- In coordination compounds, there are two types of linkages (valences) − primary and secondary.
- The primary valences are ionisable, and are satisfied by negative ions.
- The secondary valences are non-ionisable, and are satisfied by negative ions or neutral molecules. The secondary valence is equal to the coordination number of a metal, and remains fixed for a metal.
- Different coordination numbers have characteristic spatial arrangement of ions or groups bound by the secondary linkages.
Such spatial arrangements are called coordination polyhedra. The species within the square brackets are called coordination entities or complexes, and the ions outside the square brackets are called counter ions.
Difference between a Double Salt and a Complex
- In water, a double salt dissociates completely to give simpler ions. Examples of double salt: carnallite (KCl.MgCl2.6H2O), Mohr’s salt [FeSO4.(NH4)2 SO4.6H2O]
- Complex ions do not dissociate further to give simpler ions; for example, [Fe(CN)6]4−, [Fe(C2O4)3]3−.
Definition of Important Terms in Coordination Compounds
- Coordination Entity
- Constitutes a central metal atom or ion bonded to a fixed number of ions or molecules
- Example: [CoCl3(NH3)3] is a coordination entity
- Central Atom or Ion
- The atom or ion to which a fixed number of ions/groups are bound in a definite geometrical arrangement around it in a coordination entity
- Example: Ni2+ in [NiCl2(H2O)4] and Fe3+ in [Fe(CN)6]3−
- Ligands
Ions or molecules bound to the central metal atom or ion in a coordination entity
- Didentate
- Polydentate
- Ambidentate
(Can bind through two different atoms)
- Coordination Number
- Number of ligand-donor atoms bonded directly to the metal
- Example: The coordination number of Pt and Ni in [PtCl6]2− and [Ni(NH3)4]2+ are 6 and 4 respectively.
- Coordination Sphere
- The central atom or ion and the ligands attached to it are enclosed in square brackets, which are collectively known as the coordination sphere.
- Example: In the complex K4[Fe(CN)6], the coordination sphere is [Fe(CN)6]4−.
- Coordination Polyhedron
- The spatial arrangement of the ligand atoms which are directly attached to the central atom or ion
- Example: Octahedral, square planar, tetrahedral
- Oxidation Number of Central Atom
- The charge it would carry if all the ligands are removed along with the electron pairs that are shared with the central atom
- Example: Coordination number of copper in [Cu(CN)4]3− is 1.
- Homoleptic and Heteroleptic Complexes
- Homoleptic − Complexes in which the metal is bound to only one kind of donor group. Example: [Co(NH3)6]3+
- Heteroleptic − Complexes in which the metal is bound to more than one kind of donor groups. For example: [Co(NH3)4Cl2]+
Example :
The ratio of moles of AgCl precipitated on adding AgNO3 to PdCl2.4NH3 and CoCl3.4NH3respectively is
- A )
2:3
- B )
3:2
- C )
2:1
- D )
1:2
In PdCl2.4NH3, the secondary valency is 4 i.e. 4 NH3 is attached with Pd by non-ionisable valencies. Only 2Cl− are attached to Pd as primary valencies which are ionisable and precipitated out as 2 moles of AgCl.
Similarly, due to 6 secondary valencies of Co, only one Cl− is able to ionise and form 1 mole of AgCl.
Hence, the ratio of AgCl precipitated in the two complexes is 2:1.
Example :
The coordination number and oxidation state of metal atom X in the complex[X(en)2 (C2O4)]NO2are
- A )
4 and 3 respectively
- B )
6 and 2 respectively
- C )
4 and 2 respectively
- D )
6 and 3 respectively
In [X(en)2 (C2O4) ]NO2, both en (ethylene diamine) and C2O42− (oxalate) are bidentate ligands. Hence, the coordination number of X is 6.
∴ (en)2 has 4 donor atoms.
∴ (C2O4) has 2 donor atoms.
∴ Total donor atoms from two en and one 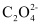 are 6.
are 6.
Let the oxidation number of X in the given complex be x.
x + 2(0) + (−2) + (−1) = 0
or, x = +3
∴ Oxidation state of X is 3.
Example :
Write the IUPAC name of the complex K2[Cr(CN)2O2(O2)NH3].
The given complex is anionic.
So, metal name is written as ‘chromate’.
The ligands are: 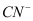 cyano
cyano
Let the oxidation state of Cr be x.
or, 2(+1) + x + 2 (−1) + 2 (−2) + (−2) + 0 = 0
or, x = 6
∴ Oxidation state of Cr is (VI).
Hence, IUPAC name of the complex is Potassium amminedicyanodioxoperoxochromate(VI).
Example :
Which of the following complexes does not show optical isomerism?
- A )
[Co(en)3]Cl3
- B )
[Co(NH3)3Cl3]
- C )
[Co(en)2Cl2]Cl
- D )
[Co(en) (NH3)2 Cl2]Cl
Optical isomerism is very common in those octahedral complexes, which have bidentate ligands. Since [Co(NH3)3Cl3] does not contain bidentate ligands, it cannot show optical isomerism.
Topics:Nomenclature of Coordination Compounds
Formulas of Mononuclear Coordination Compounds
The following are therules for writing the formulas.
- The central atom is listed first.
- The ligands are then listed in the alphabetical order.
- Polydentate ligands are also listed in the alphabetical order. In the case of abbreviated ligands, the first letter of the abbreviation is used for determining the position of the ligands in the alphabetical order.
- The formula of the entire coordination entity is enclosed in square brackets. Ligand abbreviations and formulas for polyatomic ligands are enclosed in parentheses.
- There should be no space between the ligands and the metal within a coordination sphere.
- For the charged coordination entity, the charge is indicated outside the square brackets, as a right superscript, with the number before the sign. Example: [Fe(CN)6]3−, [Cr(H2O)6]3+, etc.
- The charge of the cation(s) is balanced by the charge of the anion(s).
Naming of Mononuclear Coordination Compounds
The following rules are followed while naming coordination compounds.
- The cation is named first in both positively and negatively charged coordination entities.
- The ligands are named in alphabetical order before the name of the central atom/ion.
- Names of the anionic ligands end in −o and those of neutral and cation ligands are the same.
[Exceptions: aqua (H2O), ammine (NH3), carbonyl (CO), nitrosyl (NO)]
- To indicate the number of the individual ligands, the prefixes mono−, di−, tri−, etc., are used. If these prefixes are present in the names of ligands, then the terms −bis, −tris, −tetrakis, etc., are used. For example, [NiCl2(PPh3)2] is named as dichlorobis(triphenylphosphine)nickel(II).
- Oxidation state of the metal is indicated by a Roman numeral in parentheses.
- If the complex ion is cation, then the metal is named as the element. For example, Fe in a complex cation is called iron and Pt is called platinum.
- If the complex ion is anion, then the metal is named with ‘−ate’ ending. For example, Co in a complex anion, [Co(SCN)4]2− is called cobaltate.
- The neutral complex molecule is named as the complex cation.
IUPAC name of some coordination compounds are as follows:
[Ni(CO)4] − Tetracarbonlynickel(0)
[Co(NH3)3(H2O)3]Cl3− Triamminetriaquacobalt(III) chloride
[Pt(NH3)2Cl(NO2)] − Diamminechloridonitrito-N-platinum(II)
[CoCl2(en)2]Cl − Dichloridobis(ethane-1,2-diammine)cobalt(III) chloride
K2[Zn(OH)4] − Potassium tetrahydroxozincate(II)
Example :
Which of the following alternatives is not correct regarding the complex [Ni(CO)4]?
- A )
Oxidation state of Ni in the complex is zero.
- B )
Ni→C σ bond and C → Ni π bond are present.
- C )
Molecular geometry of the complex is tetrahedral.
- D )
IUPAC name of the complex is Tetracarbonylnickel(0).
Ni (CO)4 is an organometallic compound where metal − carbon bond is formed. M→C σ bond is formed by donation of one pair of electrons from carbonyl carbon to the vacant d-orbital of metal.
M→C π bond is formed by donation of an electron pair from d-orbital of metal to vacant
antibonding π* orbital of CO.
Topics:Isomerism in Coordination Compounds
- Stereoisomers have same chemical formula and chemical bonds, but have different spatial arrangement.
- Structural isomers have different chemical bonds.
Geometrical Isomerism
- Arises in heteroleptic complexes due to different possible geometrical arrangement of ligands
- Generally found with compounds having coordination numbers 4 and 6
- Square planar complex of formula [MX2L2] (X and L are uni-dentate) exhibits geometrical isomerism − cis-isomer and trans-isomer.
- Example − Geometrical isomers of Pt(NH3)2Cl2
- Octahedral complex of formula [MX2L4] also exhibits geometrical isomerism.
- Example − Geometrical isomers of [Co(NH3)4)Cl2]+
- Octahedral complex of formula [MX2 (L − L)2] exhibits geometrical isomerism, where L−L is a bidentate ligand. [e.g., NH2 CH2 CH2 NH2(en)]
- Example − Geometrical isomers of [CoCl2 (en)2]
- Octahedral complexes of type [Ma3b3] exhibit another type of geometrical isomerism − facial (fac) isomer and meridional (mer) isomer.
- Example − [Co(NH3)3(NO2)3]
- Facial (fac) isomer − Three donor atoms of the same ligands occupy adjacent positions at the corners of an octahedral face.
- Meridional (mer) isomer − When the positions of the donor atoms are around the meridian of the octahedron
Optical Isomerism
- Optical isomers (also called enantiomers) − Mirror images that cannot be superimposed on one another
- Chiral − Molecules or ions that cannot be superimposed
- Two forms − dextro (d) and laevo (l)
- d-isomer rotates the plane of polarised light to the right and l-isomer rotates it to the left.
- Example − ‘d’ and ‘l’ isomer of [Co(en)3]3+
→ Only cis isomer shows optical activity.
Linkage Isomerism
- Arises in the compound containing ambidentate ligand (which can ligate through two different atoms)
- Example: Thiocyanate ligand (NCS−) can bind through nitrogen to give M−NCS or through sulphur to give M−SCN.
also exhibits two forms:
- Red form − Nitrite ligand binds through oxygen (−ONO).
- Yellow form − Nitrite ligand binds through nitrogen (−NO2).
Coordination Isomerism
- Arises from the interchange of ligands between cationic and anionic entities of different metal ions present in the complex
- Example −
Ionisation Isomerism
- Arises when the counter ion in the complex salt is itself a potential ligand and can displace a ligand, which can then become the counter ion
- Example −
Solvate Isomerism
- Known as ‘hydrate isomerism’ when water is involved as a solvent
- Similar to ionisation isomerism
- Solvate isomers differ by whether or not a solvent molecule is directly bonded to the metal ion or merely present as free solvent molecules in the crystal lattice.
- Example −
(violet) and
(grey green)
Example :
Total number of isomers shown by 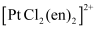 is
is
- A )
1
- B )
2
- C )
3
- D )
4
Topics:Valence Bond Theory and its Limitations & Magnetic Properties of Coordination Compounds
Valence Bond Theory
- The metal atom or ion under the influence of ligands can use its (n−1)d, ns, np or ns, np, ndorbitals for hybridisation, to yield a set of equivalent orbitals of definite geometry such as octahedral, tetrahedral, square planar, and so on.
Coordination number
|
Type of hybridisation
|
Distribution of hybrid
orbitals in space
|
4
4
5
6
6
|
sp3
dsp2
sp3d
sp3d2
d2sp3
|
Tetrahedral
Square planar
Trigonal bipyramidal
Octahedral
Octahedral
|
- These hybridised orbitals are allowed to overlap with ligand orbitals that can donate electron pairs for bonding.
- Octahedral Complexes
- The hybridisation involved can be d2sp3 or sp3d2.
- Inner-orbital or low-spin or spin-paired complexes: Complexes that use inner d-orbitals in hybridisation; for example, [Co(NH3)6]3+. The hybridisation scheme is shown in the following diagram.
- Outer-orbital or high-spin or spin-free complexes: Complexes that use outer d-orbitals in hybridisation; for example, [CoF6]3−. The hybridisation scheme is shown in the following diagram.
- Tetrahedral Complexes
- The hybridisation involved is sp3
- Example: [NiCl4]2−
- The hybridisation scheme is shown in the following diagram.
- Square planar Complexes
- The hybridisation involved is dsp2
- Example: [Ni(CN)4]2−
- The hybridisation scheme is shown in the following diagram.
Magnetic Properties of Coordination Compounds
- Complexes with unpaired electron(s) in the orbitals are paramagnetic.
- Complexes with no unpaired electron(s) in the orbitals (i.e., all the electrons are paired) are diamagnetic.
- Example: [MnCl6]3−, [FeF6]3− and [CoF6]3− are paramagnetic. It can be explained on the basis of the valence bond theory. These coordination compounds are outer-orbital complexes with sp3d2 hybridisation, and are paramagnetic containing four, five and four unpaired electrons respectively.
On the other hand, [Co(C2O4)3]3−is diamagnetic. According to the valence bond theory, it is an inner-orbital complex involving d2sp3hybridisation, with no unpaired electron(s), and is diamagnetic.
Limitations of Valence Bond Theory
- A number of assumptions are involved.
- Quantitative interpretation of magnetic data is not given.
- The exhibition of colour by coordination compounds is not explained.
- The thermodynamic or kinetic stabilities of coordination compounds are not quantitatively interpreted.
- Whether a complex of coordination number 4 is tetrahedral or square planar cannot be exactly predicted.
- Weak and strong ligands cannot be distinguished.
Example :
Which of the statements is not correct for the complex [Co(NH3)6]3+ ?
- A )
The complex is diamagnetic.
- B )
It is an inner orbital complex.
- C )
It involves sp3d2 hybridisation.
- D )
The coordination number of Co is 6.
The complex shows d2sp3 hybridisation.
Co is in +3 oxidation state and has electronic configuration 3d6.
Example :
Which of the following differences between the complexes [CoF6]−3 and [Co(NH3)6]3+ is notcorrect?
- A )
They differ in hybridisation.
- B )
They differ in magnetic property.
- C )
They differ in structural geometry.
- D )
They differ in use of orbitals for hybridisation.
Both [CoF6]−3 and [Co(NH3)6]3+ have octahedral geometry though the hybridisation of
Co is sp3d2 and d2sp3 respectively.
Topics:Crystal-Field Theory
- An electrostatic model which considers the metal−ligand bond to be ionic, which arises purely from the electrostatic interaction between the metal ion and the ligand
- Ligands are treated as point charges in the case of anions, or dipoles in the case of neutral molecules.
- The five d-orbitals in an isolated gaseous metal atom/ion are degenerate (i.e., have the same energy).
- Due to the negative fields of the ligands (either anions or the negative ends of dipolar molecules), the degeneracy of the d-orbitals is lifted, resulting in the splitting of the d-orbitals.
Crystal-Field Splitting in Octahedral Coordination Entities
Crystal-field splitting is the splitting of the degenerate energy levels due to the presence of ligands.
- The splitting of d-orbitals in an octahedral crystal-field is shown in the given figure.
- The
and
orbitals (i.e., eg set), which point towards the axes along the direction of the ligand, will experience more repulsion, and will be raised in energy.
- The dxy, dyz and dxz orbitals (i.e., t2g set), which are directed in between the axes, will be lowered in energy relative to the average energy in the spherical crystal-field.
- The energy separation is denoted by Δo (the subscript ‘o’ is for octahedral)
- The energy of two eg orbitals will increase by (3/5)Δo, and that of three t2g orbitals will decrease by (2/5)Δo.
- Spectrochemical series
Ligands are arranged in a series in the increasing order of the field strength as follows:
- Ligands for which Δo (crystal-field splitting) < P (pairing energy), are called weak-field ligands, and form high-spin complexes.
- Ligands for which Δo (crystal-field splitting) > P (pairing energy), are called strong-field ligands, and form low-spin complexes.
Crystal-Field Splitting in Tetrahedral Coordination Entities
- The splitting of d-orbitals in a tetrahedral crystal field is shown in the given figure.
- Δt = (4/9) Δo
- The orbital-splitting energies are not sufficiently large for forcing pairing, and therefore, low-spin configurations are rarely observed.
Colour in Coordination Compounds
- The colour of the coordination compounds is attributed to d−d transition of electrons.
- For example, the complex [Ti(H2O)6]3+ is violet in colour, which is due to d−d transition (shown in the figure)
- The energy of yellow-green region is absorbed by the complex, and then, the electron gets excited from t2g level to the eg level, i.e.,
- The relationships between the wavelength of light absorbed and the colour observed in some coordination entities are listed in the given table.
Coordination entity
|
Wavelength of light absorbed (nm)
|
Colour of light absorbed
|
Colour of coordination entity
|
[CoCl(NH3)5]2+
|
535
|
Yellow
|
Violet
|
[Co(NH3)5(H2O)]3+
|
500
|
Blue-green
|
Red
|
[Co(NH3)6]3+
|
475
|
Blue
|
Yellow-orange
|
[Co(CN)6]3−
|
310
|
Ultraviolet
|
Pale yellow
|
[Cu(H2O)4]2+
|
600
|
Red
|
Blue
|
[Ti(H2O)6]3+
|
498
|
Blue-green
|
Purple
|
- In the absence of ligand, crystal-field splitting does not occur; hence, the substance is colourless. For example, the removal of water from [Ti(H2O)6]Cl3 on heating renders it colourless. However, the complex [Ti(H2O)6]3+ is violet in colour.
Limitations of Crystal-Field Theory
- Anionic ligands are assumed to exert the greatest splitting effect. But the anionic ligands are found at the lower end of the spectrochemical series.
- Crystal-field theory does not take into account the covalent character of bonding between ligand and the central metal atom.
Example :
After complete dissolution of green coloured [Ni(H2O)6]2+ complex in water, ethylene diamine (en) is progressively added in molar ratio en:Ni as 1:1, 2:1 and 3:1. It is observed that green colour
- A )
does not change
- B )
changes only once
- C )
becomes colourless
- D )
changes up to 3:1 en addition
The colour of solution changes with addition of ethylene diamine (en) progressively. Ethylene diamine is a didentate ligand. In en:Ni (1:1), one en replaces two H2O from complex and forms pale blue coloured [Ni H2O]4(en)2+ complex. Similarly, colour changes up to 3:1 en addition. The final product is [Ni(en)3]2+ having violet colour.
Example :
Which of the following alternatives is correct?
- A )
In octahedral complex, t2g has higher energy.
- B )
In octahedral complex, eghas lower energy.
- C )
In tetrahedral complex, t2ghas lower energy.
- D )
In tetrahedral complex, eg has lower energy.
In tetrahedral complex, t2g has higher energy while eg has lower energy.
Eg. orbitals dx2−y2 and dz2 are not directed towards ligands. They will have lower energy while t2g orbital dxy, dyz and dxz are directed towards ligands and will have higher energy.
Topics:Bonding in Metal Carbonyls, Stability of Coordination Compounds & Applications of Coordination Compounds
Bonding in Metal Carbonyls
- Most of the transition metals form homoleptic carbonyls (compounds containing carbonyl ligands only).
- Structures of some representative homoleptic metal carbonyls are given below.
- The metal−carbon bonds in metal carbonyls have both σ and π characters.
- A σ bond is formed when the carbonyl carbon donates a lone pair of electrons to the vacant orbital of the metal.
- A π bond is formed by the donation of a pair of electrons from the filled metal d- orbital to the vacant anti-bonding π* orbital (also known as back bonding of the carbonyl group).
- The σ bond strengthens the π bond, and vice-versa.
- Thus, a synergic effect is created due to this metal-to-ligand bonding. This synergic effect strengthens the bond between CO and the metal.
Stability of Coordination Compounds
- The stability of a complex in a solution refers to the degree of association between the two species involved in the state of equilibrium.
- Stability can be expressed quantitatively in terms of stability constant or formation constant.
- For this reaction, the greater the value of the stability constant, the greater is the proportion of ML4 in the solution.
- Free metal ions are usually surrounded by solvent molecules in solution, which will compete with the ligands molecules (L) and be successively replaced by them as follows:
Where, K1, K2, …= Stepwise stability constants
- Alternatively,
Where, β1, β2, …. = Overall stability constant
The stepwise and overall stability constants are therefore related as follows:
- The reciprocal of the formation constant is called instability constant or dissociation constant.
Applications of Coordination Compounds
- In many qualitative and quantitative chemical analyses: Colour reactions are given by metal ions with a number of ligands (especially chelating ligands), which help in detection and estimation.
- Hardness of water can be estimated by simple titration with Na2EDTA, which forms stable complexes with Ca2+ and Mg2+ ions.
- Some important extraction processes of metals such as gold and silver make use of complex formation.
- Coordination compounds are used as catalysts. For example, Wilkinson catalyst, [(Ph3P)3RhCl], is used for the hydrogenation of alkenes.
- Chelate therapy is used in medicinal chemistry. For example, EDTA is used in the treatment of lead poisoning. Some coordination compounds such as cis-platin and related compounds inhibit the growth of tumours.
- Coordination compounds are of great importance in biological systems. For example, chlorophyll is a coordination compound of magnesium, haemoglobin is a coordination compound of iron and vitamin B12 is a coordination compound of cobalt.
Example :
Which of the following coordination complex is used in hydrogenation of alkenes?
- A )
Na2 EDTA
- B )
K4[Fe(CN)6]
- C )
[(Ph3P)3 RhCl]
- D )
Ziegler-Natta catalyst.
[(Ph3P)3 RhCl] is a rhodium complex, well known as Wilkinson catalyst. It is used in hydrogenation of alkenes i.e. for converting unsaturated hydrocarbons to saturated hydrocarbons.
Example :
The stepwise stability constants (k1, k 2, k 3,.... k n) and the overall stability constant (βn) in coordination complexes can be related as
- A )
- B )
- C )
- D )
We have
M is central metal atom or ion while L are ligands. Generally addition of L to M takes place stepwise. These can be represented as follows
where k1, k 2... are stepwise stability constants.
The overall stability constant can be written as
where β4 is overall stability constant.
The stepwise stability constants and overall stability constant can be related as
No comments:
Post a Comment